The Geometry of the Streets:
Why Manhole Covers are Round
• You will want to watch this short video first—and you’ll need to read all the text.
• Read •
The Geometry of the Streets:
Why Manhole Covers are Round
A Very Brief History of the Manhole
We see them every day on our streets and sidewalks, but we rarely stop to think about where manhole covers came from.
Manhole covers have a surprisingly long history that stretches back thousands of years. The ancient Romans, famous for their incredible engineering, used stone slabs to cover their massive sewer systems. These slabs kept the streets clean and safe while allowing workers to climb down for repairs.
• Roman manhole covers
However, the modern manhole cover we recognize today really took off during the Industrial Revolution in the 19th century.
As cities grew and underground systems for water, gas, and electricity became more complex, we needed a way to protect these tunnels. Cast iron became the material of choice because it is incredibly strong and heavy enough that it won’t pop out of place when a heavy wagon—or a modern car—drives over it.
Today, you can find manhole covers all over the world, from the bustling streets of New York to the historic alleys of London.
In Japan, they have turned manhole covers into works of art, featuring beautiful, colorful designs of local landmarks, animals, and regional folklore.
• Manhole covers from Osaka, Japan.
• Pokemon manhole covers, Japan.
The Mystery of the Shape
Why are most manhole covers round?
Sure, it makes them easy to roll and slide into place in any alignment, but there is another more compelling reason involving a peculiar geometric property of circles and other shapes.
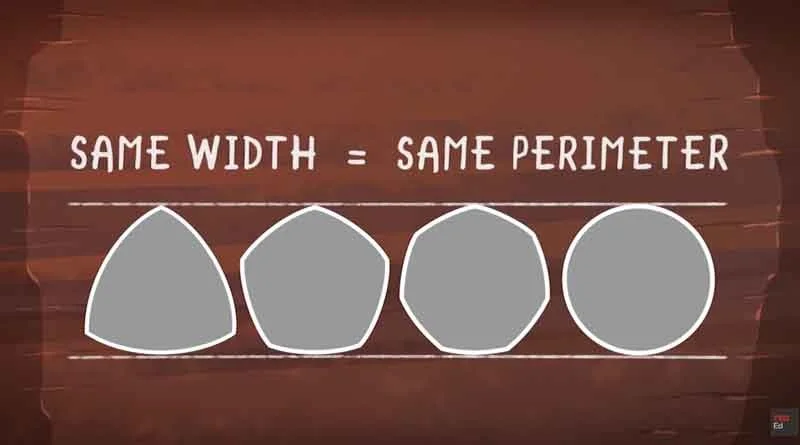
Imagine a square separating two parallel lines.
As it rotates, the lines first push apart and then come back together. This happens because the distance from the center of a square to its corners is longer than the distance from the center to its flat sides.
But try this with a circle and the lines stay exactly the same distance apart: the diameter of the circle. This makes the circle, unlike the square, a mathematical shape called a curve of constant width.
The Reuleaux Triangle
Another shape with this property is the Reuleaux triangle.
To create one, start with an equilateral triangle (a triangle where all sides are the same length). Then, make one of the vertices the center of a circle that touches the other two vertices. Draw two more circles in the same way, centered on the remaining two vertices.
The Reuleaux triangle is the space where all three of those circles overlap.
Because Reuleaux triangles can rotate between parallel lines without changing their distance, they can actually work as wheels, provided a little creative engineering is used. Since the center of the triangle moves up and down slightly as it rolls, the axle of a Reuleaux "wheel" has to be flexible or attached to a special linkage.
The Wankel Rotary Engine
One of the most famous real-world uses of the Reuleaux triangle is inside a machine called the Wankel Rotary Engine.
In most car engines, pistons move up and down in a straight line. However, in a Wankel engine, a Reuleaux triangle-shaped rotor spins inside an oval-shaped chamber.
• In a Wankel engine, a Reuleaux triangle-shaped rotor spins inside an oval-shaped chamber.
Because the triangle has a "constant width," its three points stay in contact with the walls of the engine at all times as it spins.
This creates three separate pockets of space that change size. These pockets pull in fuel, compress it to create power, and then push out the exhaust. Because the motion is circular rather than up-and-down, these engines can be very small, light, and powerful.
Drilling Square Holes
If you rotate a Reuleaux triangle while rolling its midpoint in a nearly circular path, its perimeter traces out a square with rounded corners. This allows for a very special invention: triangular drill bits that can carve out square holes!
While it might sound like science fiction, these drill bits are actually used in real-world engineering.
An inventor named Harry Watts started the Watts Brothers Tool Works over a century ago to sell these specialized bits.
Today, they are used by woodworkers and metalworkers to create "mortise" joints or to make square holes for bolts in heavy machinery.
It is a perfect example of how a "pointy" triangle can create a perfectly straight square.
Mathematical Theorems and Polygons
Any polygon with an odd number of sides can be used to generate a curve of constant width using the same method we applied earlier, though there are many others that aren't made in this way.
For example, if you roll any curve of constant width around another, you will make a third one.
To understand how these shapes work, we have to look at two important mathematical concepts: the perimeter and ∏ (Pi).
Perimeter: Think of the perimeter as the boundary of a shape. If you were an ant walking all the way around the outside edge of a shape, the total distance you walked would be the perimeter.
∏ (Pi): This is a mathematical constant that represents the ratio of a circle's circumference (its perimeter) to its diameter. It is approximately 3.14. No matter how big or small a circle is, if you divide the distance around it by the distance across it, you always get ∏ (Pi).
This collection of pointy curves fascinates mathematicians.
They have given us Barbier's theorem, which says that the perimeter of any curve of constant width, not just a circle, equals ∏ (Pi) times the diameter.
Another theorem tells us that if you had a bunch of curves of constant width with the same width, they would all have the same perimeter, but the Reuleaux triangle would have the smallest area.
The circle, which is effectively a Reuleaux polygon with an infinite number of sides, has the largest area.
Constant Width in Three Dimensions
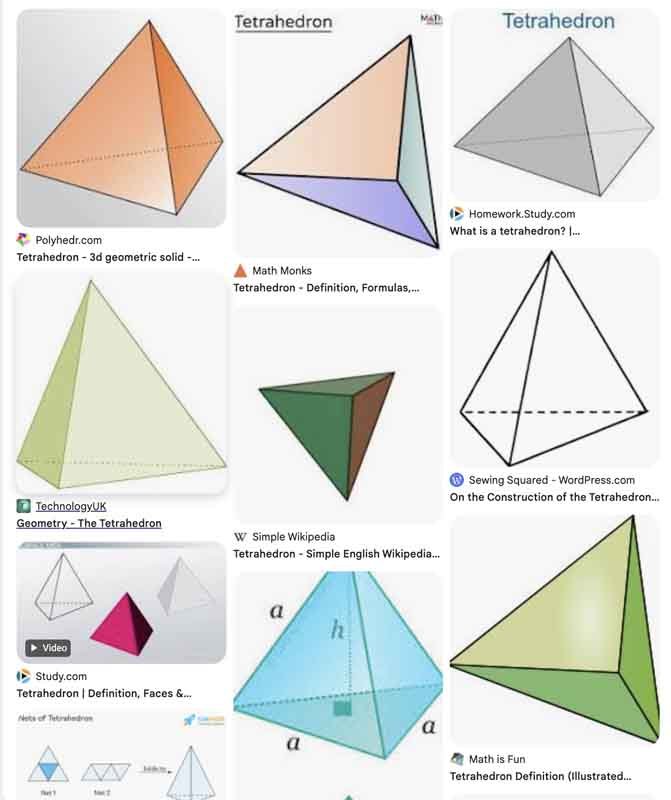
In three dimensions, we can make surfaces of constant width, like the Reuleaux tetrahedron.
To understand this, we first need to know what a tetrahedron is. A tetrahedron is a 3D shape with four faces, where each face is a triangle. It looks like a pyramid with a triangular base.
A Reuleaux tetrahedron is formed by taking a tetrahedron, expanding a sphere from each vertex until it touches the opposite vertices, and keeping only the region where they overlap.
Surfaces of constant width maintain a constant distance between two parallel planes.
This means you could throw a bunch of Reuleaux tetrahedra on the floor and slide a board across them as smoothly as if they were round marbles!
While they aren't often used for wheels because they feel "bumpy" when handled, they are sometimes used in high-tech bearings for machines that need to slide perfectly without using spheres.
Why it Matters for Manholes
Now, back to manhole covers.
A square manhole cover’s short edge could line up with the wider part of the hole (the diagonal) and fall right in! This would be incredibly dangerous for anyone working below or walking above.
But a curve of constant width—like a circle or a Reuleaux triangle—cannot fall in, no matter how you turn it.
It is always "wider" than the hole it covers. Usually, they are circular because circles are the easiest to manufacture and roll, but keep your eyes open!
In places like San Francisco, you might just come across a Reuleaux triangle manhole cover. They are rare, but they are just as safe as the round ones.
The Power of Noticing
We often walk through the world without really looking at it.
By asking a simple question like, “Why are manhole covers round?” we can open up new horizons. This one question leads us through the history of ancient Rome, the secret of drilling square holes, and the math of curves that aren’t quite circles.
The next time you see something that everyone else takes for granted, stop and ask "Why?"
You might just find a whole world of mathematics and history hidden right under your feet.
► COMPREHENSION QUESTIONS
— please answer with complete sentences
When did the modern manhole cover really take off?
When manhole covers are turned into art, what might we see on them?
List at least five things you might see.
What do we find when we compare the distance from the center of a square to its corners to the distance from the center to its flat sides?
What is a Reuleaux triangle?
Do your best to describe it.
What is one of the most famous real-world uses of the Reuleaux triangle?
What kind of polygon can be used to generate a curve of constant width?
What is Barbier's theorem?
You can write it out even if you don’t understand it!
What is a tetrahedron?
So— Explain why manhole covers are round.
Where might you find a Reuleaux triangle manhole cover?
A+ BONUS question: Tell of a time when you looked at something ordinary, something you looked at all the time, and suddenly saw something new.